Basis for the Solution Space of the Homogeneous System

Question

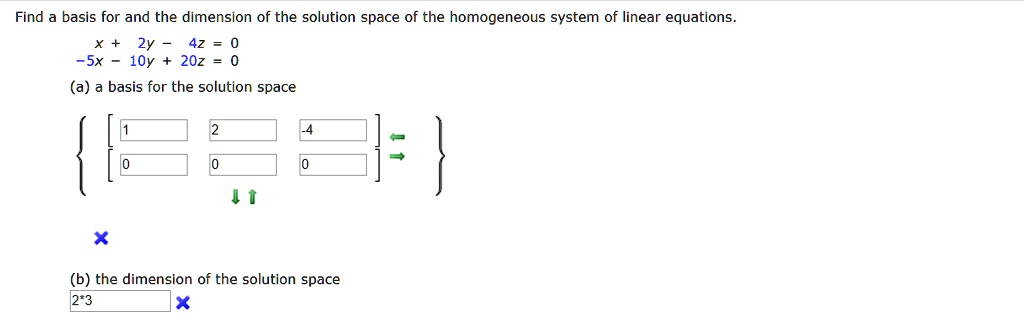
Find basis for and the dimension of the solution space of the homogeneous system of linear equations 2y 42 = ~SX 10y 20z (a) basis for the solution spacethe dimension of the solution space 2*3

Find basis for and the dimension of the solution space of the homogeneous system of linear equations 2y 42 = ~SX 10y 20z (a) basis for the solution space the dimension of the solution space 2*3

Answers

Find a basis for the solution space of the homogeneous linear system, and find the dimension of that space. $$\begin{array}{r} x_{1}-4 x_{2}+3 x_{3}-x_{4}=0 \\ 2 x_{1}-8 x_{2}+6 x_{3}-2 x_{4}=0 \end{array}$$

In order to find the basis for the set of solutions to the system of equations. We want to find a basis for the no space of this matrix A which is a coefficient matrix. So in order to do so we're going to perform elimination first. So here we have 111 So for row two we're gonna subtract three of wrote one to get zero here, a negative one And a -5. Now, for a three we're gonna subtract four of row one, So when again negative one here and a negative five. Finally, for row four, we're gonna subtract six tantra one, So we're gonna have a negative one And then a -5. So we see these last three rows are all the same afterwards. So for the next step, 111 we're going to divide the second row by negative one so that we can get a pivot of one. And then for the last two rows we're going to add one times. So road three will be itself plus wrote you and that was zero it out and see what wrote for so and then we'll have to pivots And one free variable which is extra. So we're gonna set extra equal to zero Or you go to one and then solve for X two and X one. So we have X two plus five equals zero. We get extra, goes negative five. And then we have X one plus X two Plus extra equals zero. Then we plug in X two and X three X one minus five plus one equals zero. So we get X one equals four. So we have one vector in R basis. So the dimension is one and this is a vector. Yeah.

Welcome to liberate in the current problem. We are given the equations. Excellent. Plus X two -X. Tree is equal to zero. The next depression is minus two. Excellent. Plus X two x two. Yes. Yes. Yeah. Yeah. That is Monye 6 1. That's extremely It goes to no he has from the this is that is the set of vectors that can generate the uh if you have those victors, you can generate any victor in that vector space. The first thing that we do is we write the argument. The Coefficient Matrix that is 1, 1 minus one -2 -1, two -10. But so this is the coefficient metrics. Now we will do standard reduction of operations. And we started by we start by doing a new second rope. That will be two times old. First through Plus the old 2nd drop. Okay, so we will get This into two,: -20. This into two to minus 11 the center to minus two plus two zero. And a new artery. That would be simply addition of all that one and all our three. So we will have minus one plus 101 plus 00 minus 11 oh one. Class zero one and -10. Now if you see both the second and do our thing so we can do one more this. Uh huh 010. And we didn't subtract recorded all from New R three would be our 1- archery correct? So we get this so if we again go back to the same equation for medical building X one plus X two minus X three is equals to zero and X two equals to zero. So first thing we have is extra equals to zero. Now if this is a question one from one we have X one plus zero minus extreme is equals to zero. Therefore X one minus extra is equals to zero. Therefore X one is equals to extreme. This is another inspiration. Now taking help of this and this. What we can do we can think of a basis vector which is the solution of this basis victor. Well B uh huh solution of the given set. It's given set Only this set marked by one. well marked by one. Whatever it is, it is actually the original set over here. Right? So indeed this Exxon extract through whatever we will find out to be will be solution to. That's it. Now if I as you X one equals three X three and X two is equal to zero. This is there already. And if I just as you knit X one, B. T. Any beard he belongs to the real line. Then extra is also T. Therefore the victor. The solution victory would look like X one comma X two comma X three will be T comma zero committee Credit. So if I take the common we will get 10. That means what? This shows the victor. 101 forms the basis of the given system. Are given system of equations. Okay? And The dimension since there is only one letter and since dad is only thank you since there is only one victor. The dimension. Yes. What? So I hope you could understand this. Let me know if you have any questions but by

So this question wants us to find a basis for this set of this system of equations. So that means we need to find the basis for the no space of this matrix A which is just a coefficient matrix 213 There are three unknowns and three equations. So let's perform elimination to find the no space. So first we want to swap Rose two and three because we noticed that this pivot, He's a zero and we don't want that next. We want to eliminate this value. So we'll subtract one half of real one from there. We'll have a zero here, a negative one half and 5- Treehouse, which is five halves. Five Ministry House, which is a house. Seven house. Sorry, these two rows remain. Now for our second pivot we want this to be a zero. So we'll do road three is equal to itself Plus 1/2 of road to. And that gives us 213 zero. Do you know, one plus seven Fords. So that gives 11 forts, unchanged third row. Now we see. Sorry I subtracted the wrong road. We want to keep this row and how this would be zero, seven halves plus 1/2 which is for. So Here we see we have three pivots, which means that This extreme must be zero, X two plus X three equals zero, so X two must also be zero, Then two x 1 equals zeros. So this means since there are no free variables in three pivots, that the only vector in no space is a zero vector. So the dimension of this space is equal to zero and we don't have any other vectors except for the zero vector in the no space.

To find a basis for this set of equations. We just need to find a basis for the no space. So we can have it as a matrix multiplication of A. X equals zero and then find any exes that are in the know space that are not the zero vector. So let's start with elimination. We want to subtract 5/3 of row one from road to that will give us a zero here, negative eight thirds here, negative two thirds here, Maget 8/3 here. So now we see we have two pivots which means that we have to free variables here. So we will set one of the three variables X three equal to zero here and X four equal to zero separately. So we'll have negative 8/3 x two plus minus eight thirds X four for the case when extra zero for the bottom equation and then we'll have three X one plus X two plus X four from this equation. We get that X two equals negative explore. So we put that into the bottom equation and we get three x 1 -2 x two. Now we can solve for X one Yeah X one equals two thirds X two two X two Because negative one export echo swan X one equals negative two thirds and extra equals zero. So that gives us this factor negative two thirds negative one, zero and four. Not for one. So this is one of the bases. Now for this other case we're gonna do this case now we'll have -8/3 x two minus two thirds Ignoring that last term because we set export equal to zero. So we have three X 1 plus X two plus one equal to zero. And now Here from here we have X two equals two thirds times negative 3/8. Which gives us negative 1/4. Now we can plug that into the bottom equation. So we have three x 1 Plus 3/4 Ego zero. It gives us -3/4 until number three. These canceled. We get X when he goes negative 14 so a second basis, Rector is negative 14 negative 14 one and zero. So these are two basis vectors. And the dimension is too, because we have two vectors here.

---

Similar Solved Questions

Basis for the Solution Space of the Homogeneous System

Source: https://itprospt.com/num/1913254/find-basis-for-and-the-dimension-of-the-solution-space-of

Share this post